拉普拉斯矩阵
首先考虑图的关联矩阵(incidence matrix),$C=C(G)$。其中每一列表示的是图的节点,每一行表示的图的一条边。
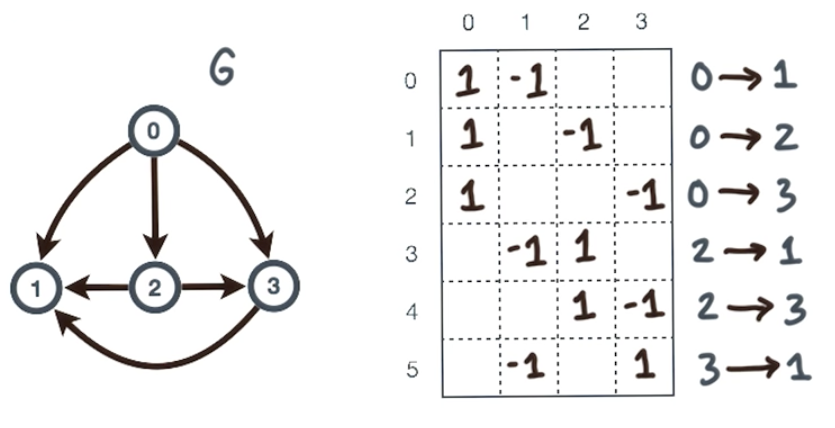
然后我们将这个关联矩阵可以写成:
其中,$e_k$是一个边向量,表达了从节点 i 到节点 j 的一条边$[\cdots, \underbrace{1}_i, \cdots, \underbrace{-1}_j, \cdots]$,其余位置都为 0。所以:
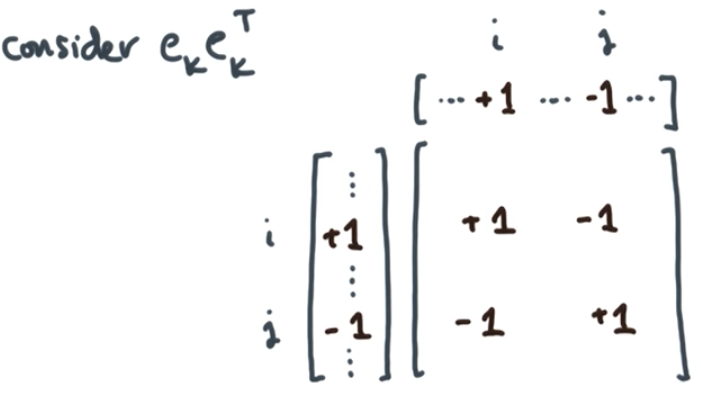
考虑上方这个矩阵,我们会发现它的对角线上,$ii$这个位置和$jj$这个位置,会都为 1,其实表达了在该图中,节点 i 和 j 位置的度数为 1。而其余两个位置$ij$和$ji$则表达了该位置存在一条边。此时,该矩阵损失了方向信息。
当对这一系列矩阵求和,我们就得到了图的拉普拉斯矩阵,对角线表达了节点的度数,而非对角线部分则是边的信息。
当然,在有权图中,上面的关联矩阵,就不应该表示成 1 和-1,而应该是边的权重的平方根。
那么,拉普拉斯矩阵就可以定义成:
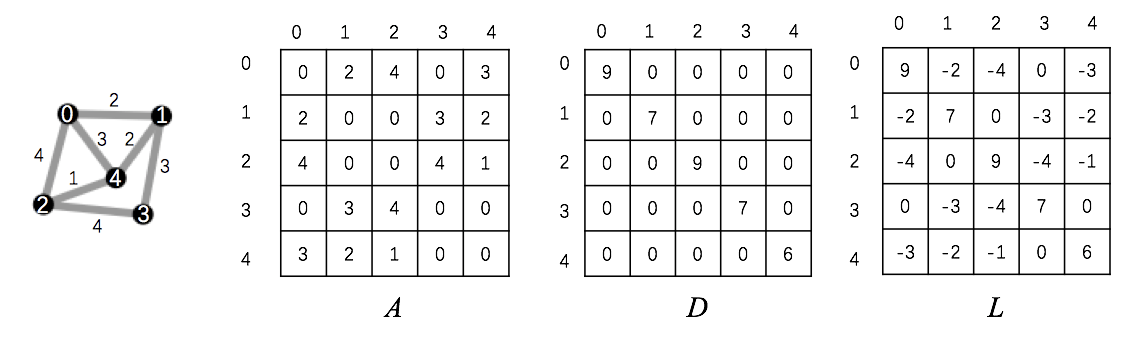
假设一个无向正权图$G=(V,E)$,其邻接矩阵表示成$A$,每个元素代表边的权重。其度矩阵表示成$D$,是一个对角矩阵,对角线的元素则是每个节点所带的连接边的权重和($d_{ij}=\sum_kw_{ik}$),这里不考虑自环。那么拉普拉斯矩阵(Laplacian)就是$L=D-A$。
弹簧模型
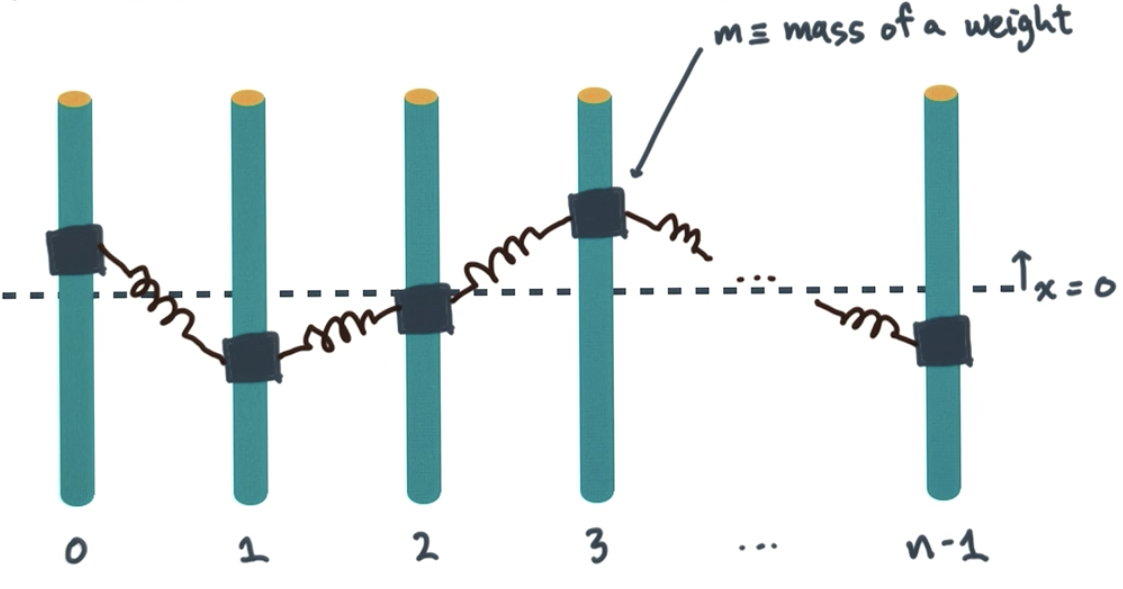
首先,假设一组固定的杆子,他们上面套上了一些可以滑动的滑块,这些滑块的质量都是$m$,滑块之间互相用弹簧链接。
当某个滑块$i$上升到$x_i$的位置时,该滑块受到的弹簧拉力应该是:$-k(x_i-x_{i-1})-k(x_i-x_{i+1})=-k(-x_{i-1}+2x_i-x_{i+1})$。根据牛顿第一定律,滑块受到的拉力又应该是$m_ia_i=m_i\frac{d^2}{dt^2}x_i(t)$
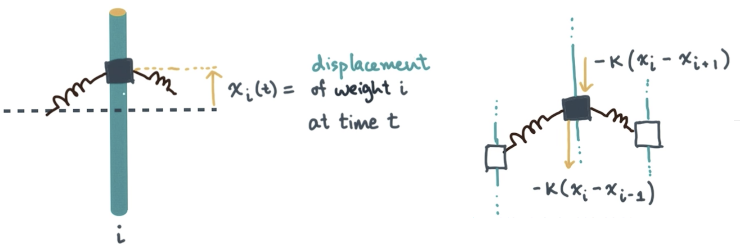
将所有滑块在时刻$t$的位置写成向量形式:
那么,拉力可以被写成:
该矩阵是一个$t \times n$列的矩阵,该矩阵就可以被看做一个$n$个点互相连接的单链条的图的拉普拉斯矩阵:
最终每个点的位置,会呈现出一种正弦波的变化趋势,事实上,这个变化趋势是由多个正弦或者余弦波的叠加组成,也就是可以通过傅里叶变化,转换为频域上的模式,每一种模式和该拉普拉斯矩阵的特征向量所给定。
代数连通性
首先介绍一些拉普拉斯矩阵的特性:
拉普拉斯矩阵是对称的。
拉普拉斯矩阵的特征值都是实数并且非负的,而且对应的特征向量都是实数并且正交的。按照惯例,会对这些特征值进行排序:$\lambda_{n-1} \geq \lambda_{n-2} \geq \cdots \geq \lambda_0 \geq 0$
如果$G$有$k$个连通子图,当且仅当:
(这一点也说明了,拉普拉斯矩阵的特征值和图的连通性有一定关联)
对于一个有$n$个点的图$G$,将该图分成正负两部分。
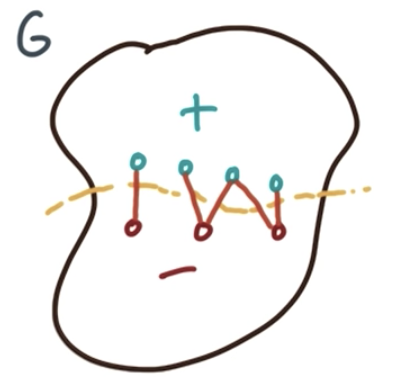
记:那么,连通+-两部分的那些切割边的数量,则可以用$\frac{1}{4} x^TL(G)x$表示。
Courant minimax principle
承接上一节,假如需要最小化正负两部分的切割边,则我们需要$min \frac{1}{4} x^TL(G)x$
定理:给定任意实向量$\vec{y}$,对$y$进行标准化,使得$y^Ty=n$,且$\sum_iy_i=0$
那么,使得$\frac{1}{4} x^TL(G)x$最小的$y$满足以下条件:
其中,$\vec{q}_1$和$\lambda_1$是拉普拉斯矩阵的第二个特征向量和对应的特征值。
于是,$G$的任意一种二分切割方法,最小只能切割出$\frac{1}{4}n\lambda_1$条切割边。
假如,我们要找到,拥有最小切割边的分割方式,我们可以:
创建$G$的拉普拉斯矩阵$L(G)$
计算该矩阵的第二个特征向量$(\lambda_1, \vec{q}_1)$
用该特征向量的正负来表达$x$,就能得到想要的分割方式。也即: